Electrodynamics of submicron dust in the cometary coma
M. K. Wallis and M. H. A. Hassan
Department of Applied Maths & Astronomy, University College, Cardiff CF1 1XL, Wales, UK
Received September 13, accepted November 26, 1982
Резюме. Електромагнітні сили, що походять від полів сонячного вітру діють суттєво на субмікронні пилинки в кометній комі. Заряд пилинки і отже сили чутливі до складу та умов у кометній плазмі, так як і до розміру пилинки. Для діелектричних пилинок 0.1 μm і провідних пилинок 0.3 μm або менше, електромагнітні сили домінують над радіаційним тиском. Сильніші прискорення, можливо, утворюють віялоподібні структури, які інколи спостерігаються. Вони можуть сприяти тому, що пилинки обійдуть щити, спроектовані, щоб захистити космічні кораблі Джотто і Вега, при їх швидкому русі через пилову кому комети Галлея.
Ключові слова: комета — місія Джотто — зарядженість пилинок - пилова кома - кометна електродинаміка
1. Вступ
Електромагнітні сили сильніші, ніж радіаційний тиск для дрібних пилових частинок порядку 0.1 μm, як було визнано Паркером (1964) і Notni (1964). Останній також підкреслив, (1964, 1966), що такі пилинки повинні бути позитивно заряджені у сонячному вітрі, і негативно заряджені у щільній кометній плазмі. Koutchmy and Lamy (1978) зробили висновок присутності малих заряджених пилинок порядку 0.1 μm у прискорених структурах в кометних хвостах, у той час як ряд авторів вивчали заряджені пилинки в міжпланетному просторі (Levy and Jokipii, 1976; Morfill and Griin, 1979; Consolmagno, 1979; Lafon et al., 1981).Моделі пилової коми комети Галлея розроблені для місії Джотто (Reinhard, 1979; Divine, 1981; Hellmich and Keller, 1981) проігнорували зерна <0.3 μm, незважаючи на кометні докази й пряме виявлення у метеорних потоках пилинок <0.1 μm (Singer and Stanley, 1979). Склад пилинок може бути частково силікатний (Ney, 1982), але високі значення тиску випромінювання (Koutchmy and Lamy, 1978) говорить про високу поширеність вуглецевих пилинок, можна припустити "C-zero" тип хондритів (Fechtig, 1981). Цілі цього якісного дослідження, по-перше, показати, що дрібні заряджені пилинки можуть бути важливим для запланованих місій і по-друге, показати, що електродинаміка зарядженої частинки є природнім поясненням асиметричних пилових структур. Просторові спостережні дослідження разом з даними про сонячний вітер необхідно опрацювати, щоб дослідити ці питання.
2. Заряд на пилинках
Повний заряд визначається шляхом накопичення електронів з плазми конкуруючи з накопиченням іонів і викидом фотоелектронів. Заряд на сферичній пиилнці радіуса a[см], пов'язаний з його потенціалом φ[V] в силу φ ∝ q/a, змінюється відповідно до рівняння потоку.
| dq/dt=Iv+Ii-Ie, q = 7⋅106φa, | (1) |
Iv=πa2eFv з Fv≅3˙1010χr-2exp−(eφ*/kTv)/cm2 s
на геліоцентричнsq відстані r[AU] з φ*=mах[&phi,0], kTv=1.3eV (Manka, 1973; Grard et al., 1973) і χ=0.9 для металевих чи графітових і 0.1 для крижаних пилинок. Накопичення електронів для розмірів a « радіуса Дебая і швидкості плазми « теплових швидкостей:
| Ie=nevth2π1/2a2W(eφ/kTe), | (2) |
Загальний вираз для W для кінцевої швидкості u був даний Notni (1964) і наново виведений Lafon et al. (1981): це вираз потрібно використовувати для опису накопичення іонів, яке однак менше, ніж накопичення електронів в порядку u/Vth,e раз. Лафон та ін. використали сучасні дані про спектр Сонця і сонячний вітер (у тому числі компонент надтеплових електронів). Notni, з іншого боку, припустив вторинне виробництво електронів і мав справу з корисно широким діапазоном параметрів, при виведенні аналогічних потенціалів у вільному сонячному вітру на 1 а.о. (а саме +5—6 В, а не +3—4 V від Лафон та ін.) Mukai (1981) включив зміни фотопоглинання зі складом пилинок і розміром, даючи утруднені χ для малих a. Він підтвердив, що параметр вторинних електронів з (2) має особливо важливе значення в стислій, гарячій плазмі сонячного вітру, як у зовнішній кометній комі, запобігаючи великим негативним потенціалам, як показано на мал. 1 з Notni.
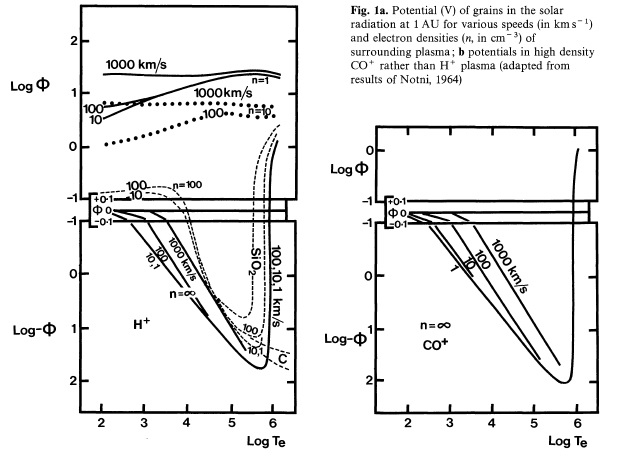
Слід визнати, що вторинна емісія менш важлива в контексті заряджання космічного апарату (Grard др., 1973; Manka, 1973), але в цьому випадку використовується модифікована форма Ie, що відповідає розміру тіла > радіус Дебая. Meyer-Vernet (1982) знову проаналізували питання виведенням багатозначних рішень для найбільш забруднених матеріалів (в &phi>0), але цей випадок не важливо для кометного мікропилу. Результати Нотні залишаються дійсними, і ми будемо використовувати їх разом з повторною оцінкою вторинних електронів і з формулами (1) та (2) для якісного керівництва.
Вторинна електронна емісія залежить від матеріалу, будучи малою в металах, але помітно перевищуючи падаючий потік Ie в ізоляторах. Notni використав наближення до експериментальних даних у формі
|
δ=δm[1-exp(-4.3E/Em)], E | (3a) |
| δ=δm(E/Em)exp[-2(E/Em)1/2+2], | (3a) |

З цим застереженням, можна використовувати (3б) для розрахунку середньої емісії від падаючого потоку електронів з максвелівським розподілом швидкостей у вигляді (для φ<0)
| <δ>=½δmexp(2+eφ/kTe) ψ(Em/4kTe) | (4) |
ψ(x)=x2∫0∞t5exp-(xt2+t)dt
При φ>0, виділені електрони повинні подолати цей потенціал і близькість поверхні електрона. Змінена форма для <δ> дана Meyer-Vernet (1982), де φ(х) також побудована. Відсікання в електронному прирості отримати від гарячої плазми може бути отримана шляхом установки <δ>=1, φ=0 в (4) і перетворення таким чином:
| kTe,1=¼Em/φ-1(2/e2δm), | (5) |
| (6) |
3. Залежність від умов плазми
Отримані потенціали φ істотно залежать від параметрів плазми в сонячному вітрі й комі. Ми дотримуємося Millet et al (1980) у розгляді двох плазмових станів: спокійного сонячного вітру (QSW) і високошвидкісних потоків (HSS). Приймемо, що щільність збільшується від поступової взаємодії з газом коми за моделлю Іp (1980; Ip and Axford, 1982) і температура отримується від адіабатичного (γ=5/3) і ударного нагріву (близько 10 еВ для QSW - Wallis, 1973) і охолодження при зіткненні
| Te ∝ exp(-Ze2/R2), Ze=2.0⋅104 km | (7) |
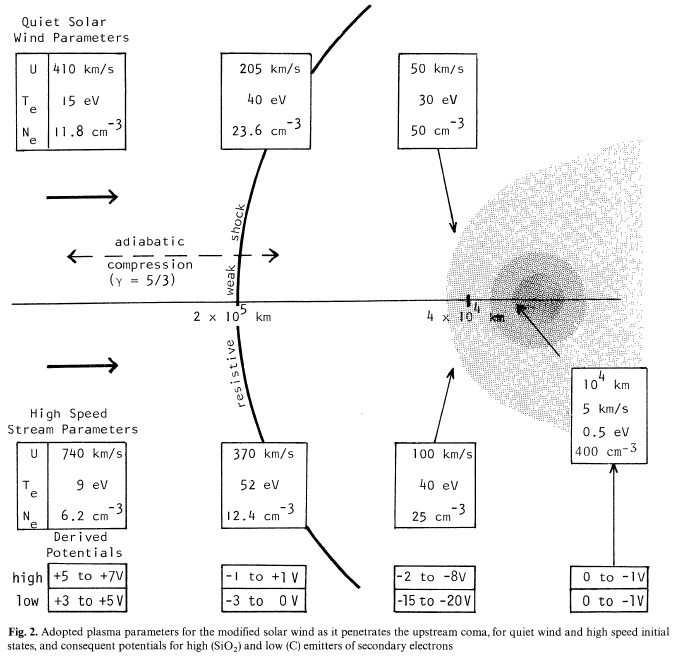
Без більш ретельного моделювання механізмів електронного охолодження та нагрівання (з турбулентними плазмових ефектів, які є непевні) неможливо бути переконливим, але ми підтримуємо знайдені Нотні негативні потенціали φ<0, у більшій частині коми і до іоносфери зіткнень в 104 км . мал 1b означає, що потенціал стає трохи більш негативним, якщо розглядати важкі іони СО+ замість протонів, але такий розгляд не включає очікуваних надтеплових кометних іонів (Wallis and Ong, 1976) які додаються вторинною емісією.
При русі пилинок назовню з внутрішньої коми, їх заряд регулює також (6) через фотоелектронні викиди на шкалі часу
| Δτ=7⋅106Δφ/(πaFν)≃30 - 300 s | (8) |
4. Динаміка пилинок
У B і E, що походять від полів сонячного вітру, заряджені пилинки намагаюся виконувати рухи з гірочастотоюΩ=10-18(φ/a2)Ωp
у величинах протонної гірочастоти Ωp(= с-1 при В=10-4G), вважаючи густину по масі пилинки 3г/см3. Таким чином для 0.1 μm пилинки, гіро-періоди близько 108с є такими довгими і гірорадіус порядку травня 5⋅1010 км так набагато більшим, ніж масштаби коми, що лінійний рух уздовж короткої дуги є хорошим наближенням:
mg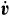 g=q(E+ g=q(E+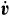 ×B)≃qE з E=-u×B ×B)≃qE з E=-u×B
| (9) |
 g≃qUB/mg=10-18ΩpUφ/a²≃0.4φ[V](a/0.1 μm)-2 cm/s² g≃qUB/mg=10-18ΩpUφ/a²≃0.4φ[V](a/0.1 μm)-2 cm/s²
| (10) |
Пилинки також підкоряються радіаційному прискоренню при g≃(а/0.1 μm)sg1 де для силікатних пилинок g1≃1.1 см/с² і S=1.7-2.0, хоча g1 вище (Burns et al., 1979) для заліза і графіту (до 1,8 і 6 см/с² відповідно до 0.1 сфери; S≃0 і g≃3 см/с² для графіту <0.03 μm). Відношення випромінювального й електродинамічного прискорень для сферичних пилинок наступне
| (11) |
Пилинки що випускаються із центрального джерела ядра з даними початковими швидкостями v0=0.3-1 км/с потоком газів, що вириваються (Wallis, 1982b). Якщо v0 береться радіальним і незалежним від кутового положення (Reinhard, 1979; Divine, 1981) і електрична сила як середнє (qE0)середнє всередині області R
| vθ=v0×(sinθ до ½sinθ) | (12) |
У випадку L0
| v1=(2|G|R1)1/2=(2R1/L0)1/2v0≃0.9-2⋅(a/0.1 μm)-1v0 | (13) |
У випадку L0>R1 (0.1 μm пилинки)
Вони пробігають позитивну область q зі швидкістю v порядку v0 і перетинають шлях Джотто з поперечним швидкостями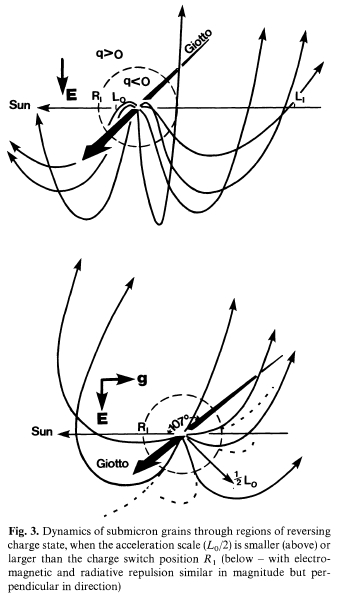
5. Висновки
На малі діелектричні (<0.1 мкм) та провідні (<0.03 мкм) пилинки суттєво впливають електромагнітні сили всієї розширеної коми та сонячного вітру, й тому поводяться зовсім інакше, ніж у простій динамічній моделі (Reinhard, 1979). Їх траєкторії через кому залежать від орієнтації магнітного поля і невизначених параметрів плазми. Діелектричні пилинки менш чутливі до радіаційного тиску, тому наповнюють набагато більше пилову кому і дають більш розмиту структури хвоста ніж графітові пилинки. Металеві пилинки залишаються негативно зарядженими довше, тому вони ще більш дифузні, поки тиск випромінювання подовжує їх витягнуту вздовж хвоста кому далі, ніж для діелектричних пилинок. Якщо такі пилинки присутні, інфрачервоні спостереження (з хорошою роздільною здатністю) яскравих пилових комет із зручною орієнтацією магнітного поля відносно лінії Земля - комета повинні дозволити, щоб коми різного складу можна було відрізнити.Вищенаведене обговорення передбачає, що сонячний вітер містить постійне магнітне поле. Якщо поле змінюється протягом дня дета́льного спостереження, як при проходженні комети кордону магнітного сектору (як це відбувається всередині ± 15 ° екліптичної широти два або чотири рази на кожне 27-денне обертання Сонця), коми бути б більш складними. У будь-якому випадку, спотворення від циліндрично-симетричні форми, викликаних самим лише радіаційним тиском, повинні бути очевидними. Пилові струмені випромінювані ядром пояснювались як неоднорідностями спостережень, так і "віялоподібними" структурами (Sekanina, 1981), але електромагнітні сили надають правдоподібне фізичне пояснення. Вісь "віяла" проходить вздовж вектора (g,(qE1)середнє/mg), недалеко від азимутального, з поширенням віяла в геліоцентричній довготі.
Що стосується місії Джотто, то з наближенням корабля до комети в площині екліптики з боку хвоста (107 ° до геліоцентричної г) він може зіткнутися з силікатними й металевими пилинками з поперечною швидкістю порядку v1 (13) і головним чином в азимутальній площині оскільки Eθ є домінуючою, цього достатньо, щоб обійти щит. Такі пилинки можуть потрапити на інструменти та секції сонячної батареї починаючи з відстані порядку L1 або кілька 106 km від ядра комети Галлея. Їх рівень виробництва й отже щільність невідомі. Divine (1981) передбачає незначну кількість пилу менше 0.2 мкм радіусу в розподілі. Екстраполюючи замість нього до менших розмірів, комети можуть виробляти пилинок 0.03-0.1 мкм з темпом 1018-1019/с. З поперечними швидкостями до 10% від Джотто, зіткнення з бортом космічного апарату можуть досягти 106-107⋅(R/1000 km)-2/m2 s. Оскільки магнітна структура сонячного вітру досить передбачувана, вона може бути практичною для зміни поточної дати прибуття корабля для мінімізації цих шкідливих впливів.
Посилання
Burns, J.A., Lamy, Ph. L., Soter, S.: 1979, Icarus 40, 1
Consolmagno, G.: 1979, Icarus 38, 398
Divine, N.: 1981, The comet Halley dust and gas environment, ESA SP-174, p. 25
Fechtig, H.: 1981, Scientific and experimental aspects of the Giotto mission, ESA SP-169,p. 47
Grard, R.J.L., Knott, K., Pedersen, A.: 1973, Photon and particle interactions with surfaces in space, ed. R.J.L. Grard, Reidel, Dordrecht, p. 163
Hellmich, R., Keller, H.U.: 1981, The comet Halley dust and gas environment, ESA SP-174, p. 31
Ip, W.-H: 1980, Astron. Astrophys. 92, 95
Ip, W.-H., Axford, W.I.: Comets, ed. L.L. Wilkening, Univ. Ariz. Press, p. 588
Koutchmy, S., Lamy, Ph.L.: 1978, Nature 273, 522
Lafon, J.-P.J., Lamy, Ph. L., Millet, J.: 1980, Astron. Astrophys. 92, 295
Levy, E.H., Jokipii, J.R.: 1976, Nature 264, 423
Manka, R.H.: 1973, Photon and particle interactions with surfaces in space, ed. R.J.L. Grard, Reidel, Dordrecht, p. 347
Mendis, D.A., Axford, W.I.: 1974, Rev. Earth Planetary Sci. 2,419
Meyer-Vernet, N.: 1982, Astron. Astrophys. 105, 98
Millet, J., Lafon, J.-P.L., Lamy, Ph. L.: 1980, Astron. Astrophys. 92, 6
Morfill, G.E., Grün, E.: 1979, Planetary Space Sci. 27, 1269
Mukai, T.: 1981, Astron. Astrophys. 99, 1
Ney, E.P.: 1982, Comets, ed. L.L. Wilkening, Univ. Arizona Press, p. 323
Notni, P.: 1964, Veröff. Sternwarte Babelsberg 15 (1)
Notni, P.: 1966, Mem. Soc. Roy. Sci. Liege 5', ser. 12, 379
Parker, E.N.: 1964, Astrophys. J. 139, 951
Reinhard, R.: 1979, The comet Halley micrometeoroid hazard, ESA-SP-153, p. 7
Sekanina, S.: 1979, Icarus 37, 420
Singer, S.F., Stanley, J.E.: 1979, Solid particles in the solar system, IAU Symp. 80, p. 329
Wallis, M.K.: 1973, Planetary Space Sci. 21, 1647
Wallis, M.K.: 1982a, Proc. ESO Workshop: The Need for Coordinated Ground-based Observations of Halley's Comet, ed. P. Veron et al., p. 171
Wallis, M.K.: 1982b, Comets, ed. L.L. Wilkening, Univ. Arizona Press, p. 357
Wallis, M.K, Ong, R.S.B.: 1976, The study of comets, NASA SP-383, p. 856
Willis, R.F, Anderegg, M, Feuerbacher, B., Fitton, B.: 1973, Photon and particle interaction with surface in space, ed. R.J.L. Grard, Reidel, Dordrecht, p. 389