Hubble Space Telescope observations of the nucleus and inner coma of comet 19P/1904 Y2 (Borrelly)
Philippe L. Lamy, Imre Toth, Harold A. Weaver (1998)
Ядро комети 19P/1904 Y2 (Borrelly) був виявлене за допомогою планетарної камери (WFPC2) з космічного телескопа Хаббла (HST). Під час наших спостережень, комета була на відстані 0.62 а.о. від Землі й 1,40 а.о. від Сонця, і мала сонячний фазовий кут 38°. Висока роздільна здатність зображень HST дозволила чітко розрізнити сигнал від ядра і сигнал від коми. Крива яскравості ядра показує, що це дуже видовжене тіло з обертовим синодичним періодом 25.0 ± 0.5 год. Якщо припустити, що ядро має геометричне альбедо 4% і є витягнутим сфероїдом з віссю обертання, що вказує в напрямку, визначеному Секаніною (1979), ми отримуємо, що його півосі є 4.4 ± 0.3 км і 1.8 ± 0.15 км. Відповідна часткова активна область ~ 8% припускає помірно активну комету. Сильно анізотропниха кома завдячує сильному направленому на Сонце віялу, а пилопродуктивність показує ознаки мінливості з часу при всіх наших спостереженнях.
1. Introduction
Нещодавно ми показали на прикладі комети 4P/Faye, що висока роздільна здатність, яку надає HST робить можливим розрізняти світло, відбите від ядра і світло, відбите від пилу в комі комети, що проходять досить близько до Землі (Lamy and Toth, 1995). Тепер ми повідомляємо про успішне виявлення ядра комети 19P/Borrelly використовуючи WFPC2, інструмент, який коригує ефекти сферичної аберації HST.
2. Observations and preliminary data analysis
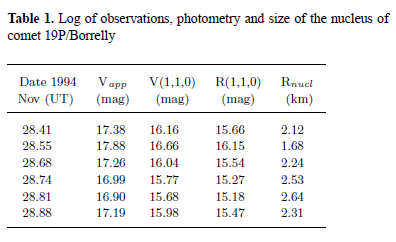
Періодична комета 19P/Borrelly пройшла в ~ 0.62 а.о. від Землі на початку грудня 1994 року, приблизно через місяць після проходження перигелію 1 листопада 1994. Під час 11-годинного інтервалу 28 листопада 1994 року, ми провели шість спостережень комети за допомогою WFPC2 в режимі планетарної камери з F675W фільтром, який має ефективну довжину хвилі ~ 670 нм і ширину смуги 89 нм. Чотири зображення були зроблені під час кожного спостереження: два з експозицією 10 сек і два з експозицією 30 сек, і всі вони були зроблені в проміжок часу 7 хвилин. Таблиця 1 перераховує дати спостережень, які відповідають серединам чотирьох послідовних зображень. Геліоцентрична відстань (r), геоцентрична відстань (Δ), і сонячна фазовий кут (α) комети практично не змінюються протягом цих спостережень на 1.401 AU, 0.622 AU, і 38°, відповідно. Пікселі WFPC2 є квадратами 0.''0455 на стороні, що проектується на відстань 20.5 км на кометі.
Наш вибір F675W фільтра — замість F702W фільтра, який використовувався для P/Faye — був мотивований чудовою фотометричною точністю. В якості первинного фільтра WFPC2, він одержує користь від докладних, обширних калібрувань, і перетворень для стандартних (Ландольта) R величин, що вимагає тільки V-R колір об'єкта, а не і V-R і V–I, як це потрібно для F702W фільтра, що вводить додаткову невизначеність.
Всі зображення були оброблені з використанням Планової наукової системи обробки даних в Інститут космічного телескопа. Вплив космічних променів був видалений за допомогою стандартного методу, заснованого на дублюванні зображення. Ретельне вивчення чотирьох зображень, отриманих в ході кожного з шести відвідувань з використанням х і у профілів через піксель максимального сигналу не виявило детектованих зрушень між ними. Ці результати, що охоплюють короткочасову послідовність (7 хвилин) і чудову здатність відстеження HST, які ми тепер перевірити на кількох кометах. Отже, чотири зображення в кожному візиті були спільно додані для збільшення відношення сигнал-шум, що дає загальний ефективний час витримки 80 сек. Єдиним винятком є шосте спостереження, для якого була невідповідність частки пікселя між окремими зображеннями, в результаті зміни орієнтирних зірок. Отже, ми окремо обробляються дві довгі витримки (експозиції) для шостого спостереження.

Порівняння нових WFPC2 зображень 19P/Borrelly з останніми WFPC зображеннями комети 4P/Faye показали вражаючі відмінності, зокрема повну відсутність сферичної аберації в WFPC2 зображеннях і сильну анізотропію коми, яка мала яскраво виражене пилове віяло в сонячному напрямку (рис. 1).
Ключовий аспект аналізу даних — правильно відділити сигнал ядра від коми. Наш попередній підхід підгонки відповідної моделі комети до зображення, беручи до уваги Функцію розсіювання точки (PSF) телескопа, залишається в силі. Тим не менш, його практична реалізація була радикально змінена, щоб впоратися з новою виправленою, PSF телескопа, а також зі складною морфологією коми 19P/Borrelly. Точне знання PSF має особливе значення. Ми використовували версію 4.0b програмного забезпечення TinyTIM написаного Krist (1995). Ця версія включає в карти дзеркальної зональної помилки, отримані з фази пошуку даних на орбіті WFPC2 і переглянутих специфікацій аберації, які значно покращують моделі PSF в порівнянні з попередніми версіями. Використовуючи це програмне забезпечення, PSF можуть бути створені на більш дрібні, ніж вибірки детектора пікселя, це явна перевага при роботі з підпробними даними WFPC2 і можливими наслідками субпіксельних ефектів. Всі PSF використані в цьому дослідженні, були розраховані для фактичних місцезнаходжень ядра на чіпі WFPC2.
Для того, щоб оцінити відносний внесок ядра і коми в спостережувані сигнали в центральних пікселях, ми провели попередній експеримент з використанням простої моделі, в якій поверхнева яскравість коми зменшується, як p−1, де p — проекційна відстань між прямою видимістю і ядром, і розподілом світла від ядра описується PSF. Це ситуація, яка повинна застосовуватися, коли є стійкий стан, сферично симетричним відтік пилу з ядра з постійною швидкістю. Відповідний повний розподіл яскравості поверхні задається: B(p)=[kc/ρ+knδ(p)]⊗PSF
де δ(p) це Діракова функція δ — функція, ⊗ — оператор згортки.
На основі сирої модельної підгонки щодо кількох зображень, ми змогли зробити наступні висновки:
i)Ядро неоднозначно виявляється.
ii)Сигнал від ядра падає до незначних рівнів на кометоцентрической відстані ~ 100 км (~ 0.''22), звідки випливає, що сигнал за цією точкою по суті весь від коми.
iii)Градієнт в профілі поверхневої яскравості коми (-1 в даному випадку) залежить від PSF тільки в радіусі ~ 120 км.
iv)Субпіксельна специфікація ядра значно покращує підгонку моделі до даних.
v)Ця проста модель, очевидно, не забезпечує адекватного опису сильно анізотропної коми 19P/Borrelly.
3. The coma model
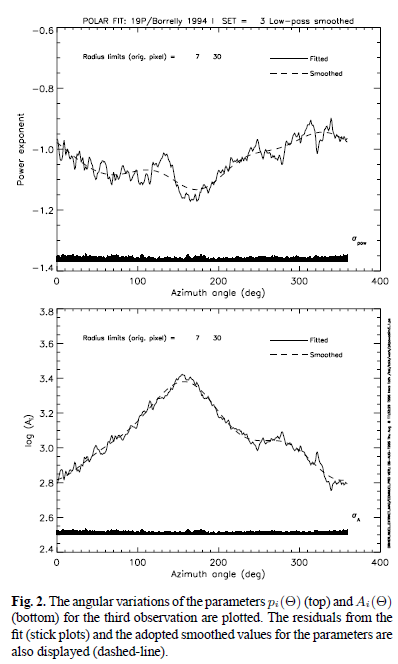
Враховуючи недоліки, описані вище, ми розробили вдосконалену модель, яку ми зараз докладно опишемо. Перший крок полягає в побудові моделі анізотропної коми, використовуючи спостережні просторові профілі яскравості. Шум у зовнішній частині коми, де спостережний сигнал ослаб, був зменшений за допомогою застосування фільтра зворотного градієнта, який зберігає нахил розподілу яскравості. Ми тоді виконуємо полярне перетворення зображень з центром на ядрі (піксель, який має найбільший сигнал) з кутовою роздільною здатністю 1° (тобто було створено 360 профілів). Кожна з 360 ліній в полярному зображенні може бути представлена за степеневим законом Bi(p)=Aippi, i ∈ [1;360] 2 × 360 параметри, Ai, pi були визначені методом найменших квадратів підібраних до спостережних профілів в обмеженому інтервалі, який містить "незабруднену" кому. Зокрема, ми використовували регіон, визначений як 140≤ p ≤600 км, щоб підібрати параметри коми, де внесоку в сигнал від ядра було знехтуваним і градієнт був по суті не залежним від згортки з PSF. Рис. 2 показаний приклад кутових варіацій Ai, pi та ілюструє як сильну анізотропію коми так і чітке відхилення від канонічного закону p=-1. Відзначимо, що пригонка коми чудова, як показують невеликі залишки, що відображаються на малюнку.
Повна модель коми зараз будується в припущенні, що описане вище параметричне представлення має місце і для p <140 км. Невеликі відмінності в підібраних параметрах були відфільтровані (див. 2), так як вони можуть бути артефактами нашого перетворення координат і, в кожному разі, не мають ніякого відношення до визначення розміру ядра. Модельні зображення коми були отримані на у 8 разів більш дрібній сітці, ніж оригінальні WFPC2 пікселі. На цьому новому масштабі, в якому субпікселі проектуються на лінійну відстань в кометі ~ 2.6 км, ефект кінцевого розміру ядра може бути введений. Наш попередній аналіз, п. 2, показав, що ядро мало ефективний радіус 2,5 км, тому ми припустили, що ця субпіксельна область 2 × 2 визначає місце розташування ядра. Для всіх пікселів, крім тих, що містять ядро, полярні координати були розраховані з декартових координат і відповідні параметричні закони були використані для розрахунку сигналу коми в кожному суб-пікселю. Чотири суб-пікселі, що містять ядро не встановлюється на нуль, але до половини середнього значення оточуючих пікселів, оскільки половина лінії прямої видимості заблокована ядром. У той час як фактичний внесок коми до суб-пікселів, що містять ядро може дещо відрізнятися від нашого рецепта, отримана величина ядра слабко залежить від точного вибору, бо суб-пікселі настільки менші, ніж дійсний WFPC2 піксель (тобто, існує значний ефект розбавлення). Крім того, згортки з PSF вимиває дрібні деталі, як показано на рис. 3. Відзначимо, що центр ядра не обов'язково збігаються з оптико-центром коми, як очікувалося для анізотропної коми. Цей ефект був наочно показаний на зображеннях високої роздільної здатності комети Галея, отриманих за допомогою камери GIOTTO/HMC (Келлер та ін 1994); в обох випадках (Галлея і Борреллі) розподіл яскравості має перекіс у бік Сонця внаслідок посиленого викиду пилу з південно-сонячної області.
Нарешті, кожна модель коми була згорнута з PSF, з якої були також взяті проби на дрібній сітці, використовуючи крихітні програмне забезпечення TinyTIM, яке обговорюється в п. 2.
4. The retrieval of the nucleus
Повна модель зображення комети отримується шляхом накладення ядра на модель коми, яка описана вище. Ядро представляється масштабованою функцією розсіяння точки, knPSF. Щоб зрозити порівняння зі спостережуваними зображеннями, модель зображення повинне бути інтегроване протягом 8 × 8 суб-пікселів, щоб відновити вихідний піксел WFPC2. При виконанні цієї інтеграції, ми дозволили 64 різних можливостей, які відповідають 64 можливим місцям ядра (хn, уn) на субдискретизованій сітці. Розташування ядра і коефіцієнт масштабування kn були визначені шляхом мінімізації залишків Q (хn, уn, kn) між модельними і спостережними зображеннями:
5. Discussion of errors
6. Properties of the nucleus
7. Properties of the coma
8. Conclusions